07/08/2011
Interstices - La modélisation des procédés biologiques de dépollution
L'activité humaine conduit au rejet dans la nature de grandes quantités d'éléments chimiques, nuisibles en général, mais qui constituent une nourriture de choix pour les micro-organismes. Ces micro-organismes se développent alors, parfois de façon excessive. Le principe de la dépollution biologique est simple : il consiste à faire comme la nature, mais de façon contrôlée, en utilisant la modélisation.
Certes, il est très difficile de modéliser le processus de dépollution. D'autant plus difficile que des pressions accrues s'exercent sur la recherche, pour qu'elle obtienne des résultats à court terme.
Pour en avoir une idée, transportons-nous au début d'un XVIIe siècle imaginaire et anachronique, mais terriblement plausible.
La suite à lire sur cette page :
http://interstices.info/jcms/c_18128/la-modelisation-des-...
(article complet, repris partiellement ci-dessous, après le commentaire )
Les risques induits par une polarisation des budgets de recherche sur des applications et la production de brevets
C’est très simple : sous prétexte de compétition, il devient plus probable de passer à côté de véritables découvertes, donc de retarder les bonnes solutions et de faire perdurer les mauvaises solutions, car à l’évidence, étant moins bonnes, elles auront couté beaucoup plus cher !
Prenons le cas des OGM et évitons de nous poser les questions habituelles de leur dangerosité qui occulte cet autre aspect qui repose sur le bon sens : en implantant une fonctionnalité dans une plante, on répond à un et unique besoin déjà satisfait par des méthodes classique et mis en avant pour des raisons de gain productivité à court terme; il n’y a pas d’innovation à proprement parlé si ce n’est à la marge (plante qui consomme moins d’eau par ex); en aucun on ne change les comportements humains de base, ni ne fait-on face à des menaces plus globales, plus lourdes de conséquences, comme une évolution du moyenne du climat de +2°. En revanche le maintien d’agricultures traditionnelle, qui brasse des multitudes de pratiques et un spectre plus larges de produits, sans parler de la nature et de sa biodiversité qui offre un réservoir de possibilités inexploitées encore plus grand, si on ne le détruit pas, présentent de façon évidente des capacités d’adaptation plus lentes mais aussi plus larges et plus sûres (les interventions trop rapides de l’homme, pour corriger les erreurs précédentes accroissent les risques de déstabilisation des chaînes d’écosystèmes, et donc mettent en péril notre propre environnement, donc nos vies) !
Revenons à la modélisation des procédés biologique de dépollution et à l’article. On pourra y voir qu’en dépit des difficultés soulevées, ‘à toutes choses malheur est bon”, il y a un aspect intéressant dans ces recherches appliquées, c’est celui de l’amélioration des instruments de mesure, étape indispensable pour faire évoluer la science non appliquée ! Qu’on en juge :
Suite ARTICLE
[…]
Que cherchons-nous à modéliser ?
La modélisation d'un phénomène consiste à le réduire aux lois mathématiques qui en rendent compte, par exemple la conservation de la masse, la loi de la gravitation, la loi des gaz parfaits. Ces lois se traduisent en équations qui autrefois étaient « résolues » à la main et maintenant le sont grâce à des ordinateurs de plus en plus puissants. C'est par exemple ce qui est fait dans les modèles physico-chimiques du réchauffement climatique. Mais il y a d'énormes difficultés à faire entrer dans les modèles les composantes biologiques d'un problème. C'est que, dans la plupart des cas, les « équations du vivant » ne sont pas connues. Et c'est en grande partie le cas dans le traitement biologique des eaux usées.
Les eaux usées contiennent en quantités parfois très importantes des éléments chimiques produits par l'activité humaine, comme les phosphates et les nitrates. Rejetés dans la nature, ils sont considérés comme nuisibles, mais constituent une nourriture de choix pour les micro-organismes qui se développent alors de façon excessive dans les lacs, les rivières, les bordures des mers, au détriment de formes de vie plus complexes qui peuvent avoir un intérêt économique important. Le principe de la dépollution biologique est simple. Il consiste à faire comme la nature, mais de façon contrôlée, c'est-à-dire à faire croître les micro-organismes indésirables dans un espace confiné, comme le bassin d'une station d'épuration.
La modélisation d'un procédé de dépollution biologique repose donc essentiellement sur les lois de croissance des micro-organismes. Que savons-nous à ce sujet ?
De la croissance des populations de micro-organismes…
Les micro-organismes unicellulaires consomment des espèces chimiques dont ils tirent l'énergie (éventuellement avec l'aide de la lumière dans le mécanisme de la photosynthèse) et la matière nécessaires à leur croissance, qui se termine par une division cellulaire. On appelle substrat ces ressources nutritives provenant de la pollution. Comprendre les relations entre les quantités de substrat absorbées et les vitesses de croissance est capital mais impossible à réaliser au niveau individuel. Comment mesurer l'accroissement de la masse d'une bactérie de la taille d'un micron ? C'est ici qu'interviennent les modèles de la dynamique des populations.
En faisant l'hypothèse, très raisonnable, que tous les individus d'une même espèce sont pratiquement identiques et l'hypothèse, plus problématique, nous y reviendrons, que tous les individus ont un accès identique aux ressources nutritives, on peut remplacer la mesure de la croissance d'un individu par la mesure de la croissance de toute une population. Ainsi, en déposant quelques individus sur un gel, on peut observer à l'œil nu le développement de la colonie sous la forme d'une tache de plus en plus grosse.
Pour identifier efficacement les paramètres d'un modèle de croissance des micro-organismes, compte-tenu de la quantité de substrat disponible, des chercheurs, Jacques Monod d'une part et Aaron Novick et Leo Szilard d'autre part, ont mis au point un dispositif expérimental appelé chémostat. Ce dispositif fonctionne comme un « réacteur » alimenté par un liquide contenant le substrat en concentration constante. Dans le réacteur, supposé « parfaitement homogène », les micro-organismes consomment le substrat et le volume est maintenu constant grâce à un débit sortant égal au débit d'entrée.
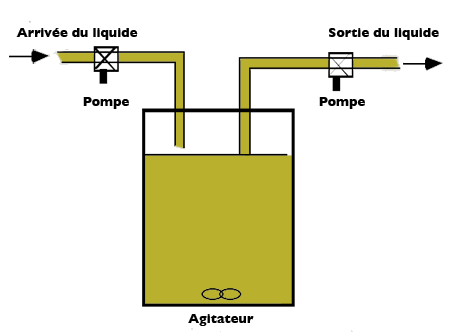
Schéma de principe du chémostat.
À ce dispositif expérimental correspond un modèle mathématique de l'accroissement relatif de la quantité de micro-organismes. La quantité de micro-organismes présents dans le volume à chaque instant est notée X. Le « taux de croissance » des micro-organismes (leur croissance rapportée à leur masse totale) est une fonction de la quantité de substrat disponible, notée S. Cette fonction est appelée « modèle de Monod ».
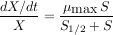
[…]
… aux procédés de traitement des eaux

Un réacteur de dépollution.
En première approximation, un procédé de traitement des eaux ne serait qu'un « gros » chémostat. Par conséquent, le modèle qui a donné de bons résultats pour comprendre la croissance d'une population isolée dans les conditions du laboratoire sera extrapolé sans vergogne à tout l'écosystème microbien en place dans un réacteur de dépollution.
Ainsi, le substrat sera considéré dans son ensemble, toutes espèces chimiques confondues. De même, l'ensemble des micro-organismes présents dans le réacteur, toutes espèces confondues, sera appelé biomasse. La concentration de biomasse naturelle, mélangée à la pollution et présente à l'entrée du procédé, sera également mesurée. La variation du substrat sera alors considérée comme égale à la quantité de substrat qui entre dans le réacteur, moins ce qui en sort, moins ce qui est consommé par la biomasse. La variation de biomasse, quant à elle, sera considérée comme égale à la quantité de biomasse qui entre dans le réacteur, plus la quantité de substrat consommée par la biomasse dans le réacteur, moins la quantité de biomasse qui sort du réacteur. La quantité de substrat consommée est calculée par une fonction qui décrit le taux de croissance de la biomasse, il peut s'agir d'un modèle de Monod, mais pas nécessairement.
[…]
Trouver les bonnes équations : la modélisation qualitative
[…]
Une nouvelle piste : la ratio-dependence
[…]
La ratio-dépendance dans les modèles de compétition
[…]
La démonstration expérimentale, solution de tous les problèmes ?
La démonstration expérimentale de la ratio-dépendance sera-t-elle la solution de tous les problèmes de dépollution biologique ?
On se doute bien que non ! Finalement, un réacteur biologique de dépollution est un écosystème d'une inimaginable complexité. Des centaines d'espèces ayant des fonctions différentes sont présentes. Certainement, aucun des deux modèles que nous venons d'évoquer à propos de la ratio-dependence, que ce soit la chaîne trophique, organisation purement verticale, ou la compétition pour une ressource, organisation purement horizontale, ne reflète à lui seul correctement la réalité.
En réalité, les niveaux trophiques ne sont pas nettement séparés (un prédateur en compétition avec un autre sur une ressource peut aussi être un prédateur de ce prédateur), certaines espèces produisent des molécules qui peuvent être consommées par d'autres, loin d'être des individus mobiles et isolés, les bactéries s'organisent et fabriquent des biofilms, sortes de matrices à l'intérieur desquelles elles circulent. Et puis, nous n'avons pas parlé des virus qui viennent compliquer la donne. Enfin ces cellules, qui certes ne sont pas des êtres vivant au Q.I. très développé, sont quand même munies de moyens de communication.
Nous sommes décidément bien loin du modèle du chémostat et de quelques avatars plus ou moins complexes. Nous pourrions continuer à développer longtemps cette vision et alimenter ainsi le double discours pessimiste auquel nous sommes souvent confrontés. Celui des mathématiciens : « toutes ces choses sont belles et fascinantes, mais bien trop compliquées pour que nous puissions en dire quoi que ce soit de mathématiquement propre » et celui des biologistes : « votre modèle est simpliste, il ne tient pas compte de tel fait capital ».
À ce pessimisme, nous opposons invariablement les quelques arguments qui nourrissent notre optimisme.
- Faire un modèle d'un procédé de traitement des eaux, ce n'est pas faire un modèle qui répondra à toutes les questions de biologie et d'écologie théorique, mais plus modestement, aider à répondre à quelques questions concrètes comme : « pour tel procédé, est-il préférable de travailler avec un seul réacteur ou deux réacteurs en cascade ? »
- C'est une évidence de dire que c'est parce qu'ils développent des instruments nouveaux d'observation des écosystèmes microbiens que les microbiologistes peuvent nous parler de leur complexité. Mais ces instruments (SSCP
 , etc.), même s'ils sont encore très imparfaits, permettent de suivre l'évolution de certains écosystèmes en continu et en laboratoire. C'est une situation très nouvelle en écologie théorique. On peut penser qu'elle sera féconde.
, etc.), même s'ils sont encore très imparfaits, permettent de suivre l'évolution de certains écosystèmes en continu et en laboratoire. C'est une situation très nouvelle en écologie théorique. On peut penser qu'elle sera féconde. - Il est maintenant possible de faire des modèles de petits écosystèmes, où chaque cellule est représentée individuellement avec la liste de ses attributs fonctionnels et de faire tourner l'ordinateur pour en obtenir une simulation. La difficulté est d'interpréter correctement les résultats de la simulation. Des équipes y travaillent et elles progressent.
- Nul n'est à l'abri d'une bonne surprise. Peut-être qu'un changement radical de point de vue éclairera considérablement le paysage.
À vrai dire, si nous devions avoir quelque pessimisme, il viendrait plutôt des conditions dans lesquelles la recherche s'exerce de nos jours. Nous avons montré à quel point notre travail, dont la finalité est on ne peut plus concrète, dépend de façon cruciale d'avancées de ce qu'on appelle la recherche fondamentale. Il est probablement bon de le répéter car, aujourd'hui, au nom de la « demande sociale », la science semble devoir massivement s'orienter vers la recherche appliquée, ou à la rigueur rester fondamentale, mais certainement jamais les deux à la fois, alors que ces deux aspects ne vont pas l'un sans l'autre. Chaque époque a ses obscurantismes.
Pour en savoir plus, nous vous proposons quelques références d'articles scientifiques ![]() .
.
14:00 Publié dans A quoi ça sert, Biologie, Math | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook |
Facebook |  Imprimer
Imprimer
07/10/2009
Biostatistiques - Que dit la loi normale ?
- que les valeurs d'une grandeur observée ou mesurée sur une population se groupent autour d'une valeur moyenne
- que les valeurs mesurées qui s'écartent de plus en plus de la moyenne sont les moins fréquentes: la probabilité d'un écart grand décroit d'autant plus rapidement que cet écart par rapport à la moyenne est plus grand.
- que si on porte dans un repère orthonormé, en abscisse les mesures, en ordonnée la fréquence d'une mesure donnée dans la population étudiée, la courbe obtenue est une courbe en cloche où le maximum est atteint pour une valeur de l'abscisse d'autant plus proche de la moyenne que la courbe se rapproche de la courbe de GAUSS caractéristique de la loi de probabilités dite loi normale.
- Quand on construit une courbe de fréquence des mesures comme ci-dessus, la forme en cloche permet de dire que la population étudiée est homogène vis à vis de la grandeur mesurée.
- Si au contraire on obtient une courbe avec plusieurs maxima (pluriel de maximum), la population étudiée n'est pas homogène, on peut assez souvent diviser la population en autant de sous groupes que de maxima, chacun de ces groupes donnant un courbe qui se rapprochent de la courbe en cloche.
- La loi normale définie à partir d’estimations de la moyenne des mesures sur la population et de la moyenne des écarts au carré par rapport à la moyenne (la variance) de ces mesures, permet de construire une courbe de GAUSS qu’on peut compare à la loi empirique obtenue avec les données rapportées à un repère orthonormé comme décrit ci-dessus, pour savoir ci cette dernière peut être correctement approximée par une loi normale.
15:51 Publié dans Biologie, Statistique | Lien permanent | Commentaires (0) |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook |
Facebook |  Imprimer
Imprimer
02/10/2009
Disparition des espèces et PAGERANK de GOOGLE
Le modèle de calcul du PAGERANK de GOOGLE évoqué dans L'idée de génie de Google : résoudre un système de n équations à n inconnues permet d’attribuer aux pages WEB, un poids fonction de leur importance mesurée en comptant les liens hypertextes qui pointent d’une page à l’autre.
Les biologistes de l'université de Californie à Santa Barbara, ont eu l’idée de reprendre ce concept pour modéliser l’interdépendance des espèces et étudier ce qui se passe dans la chaine alimentaire quand un certains nombre d’entre elles disparaissent...
Ecoutez l’extrait de l’émission “Toile du Web” passée sur France Culture ce 2 octobre 2009 pour en apprendre un tout petit peu plus…
23:55 Publié dans A quoi ça sert, Biologie, Math | Lien permanent | Commentaires (0) | Tags : disparition especes, pagerank, toile du web, france culture |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook |
Facebook |  Imprimer
Imprimer




